1. Probabilidad Condicionada. Sucesos Dependientes E – Manolomat – En el fascinante mundo de las probabilidades, la probabilidad condicionada y los sucesos dependientes desempeñan un papel crucial. 1. Probabilidad Condicionada. Sucesos Dependientes E
-Manolomat nos sumerge en este ámbito, explorando conceptos fundamentales y aplicaciones prácticas con un estilo científico y objetivo.
Al aventurarnos en este viaje probabilístico, descubriremos cómo la probabilidad de un suceso puede verse afectada por la ocurrencia de otro suceso relacionado. Profundizaremos en las características distintivas de los sucesos dependientes y su papel en diversos aspectos de la vida.
Probabilidad Condicionada: 1. Probabilidad Condicionada. Sucesos Dependientes E – Manolomat

La probabilidad condicionada mide la probabilidad de que ocurra un suceso dado que ya ha ocurrido otro suceso relacionado. Esta medida de probabilidad se utiliza para modelar situaciones en las que la probabilidad de un suceso depende de la ocurrencia de otro suceso.
Por ejemplo, supongamos que lanzamos una moneda dos veces. La probabilidad de obtener cara en el primer lanzamiento es de 1/2. Sin embargo, si sabemos que obtuvimos cara en el primer lanzamiento, la probabilidad de obtener cara en el segundo lanzamiento cambia. Esto se debe a que el resultado del primer lanzamiento influye en el resultado del segundo lanzamiento.
La fórmula para calcular la probabilidad condicionada de un suceso A dado que ha ocurrido un suceso B es la siguiente:
P(A|B) = P(A y B) / P(B)
Donde:
- P(A|B) es la probabilidad condicionada de A dado B
- P(A y B) es la probabilidad de que ocurran tanto A como B
- P(B) es la probabilidad de que ocurra B
La probabilidad condicionada se utiliza en una amplia variedad de aplicaciones, incluyendo la ciencia, la ingeniería y la medicina. Por ejemplo, los médicos utilizan la probabilidad condicionada para diagnosticar enfermedades y predecir el riesgo de desarrollar enfermedades en el futuro.
Sucesos Dependientes
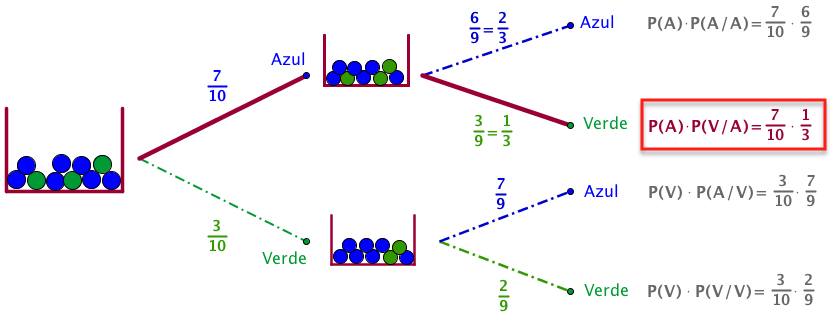
Los sucesos dependientes son sucesos cuya probabilidad de ocurrencia depende de la ocurrencia de otro suceso. Por ejemplo, el suceso “obtener cara en el segundo lanzamiento de una moneda” es dependiente del suceso “obtener cara en el primer lanzamiento de una moneda”.
Los sucesos dependientes se pueden contrastar con los sucesos independientes, que son sucesos cuya probabilidad de ocurrencia no depende de la ocurrencia de otro suceso. Por ejemplo, el suceso “obtener cara en el lanzamiento de una moneda” es independiente del suceso “obtener cara en el lanzamiento de otra moneda”.
Ejercicios y Problemas

Para practicar y reforzar los conceptos de probabilidad condicionada, a continuación se presenta una tabla con ejercicios y problemas.
Cada problema incluye un enunciado claro y una solución detallada. Sigue las instrucciones proporcionadas para resolver los problemas y mejorar tu comprensión de la probabilidad condicionada.
Ejercicios, 1. Probabilidad Condicionada. Sucesos Dependientes E – Manolomat

| Enunciado | Solución |
|---|---|
| Una caja contiene 3 bolas rojas, 2 bolas azules y 1 bola verde. Si se extrae una bola al azar, ¿cuál es la probabilidad de que sea roja dado que no es azul? |
|
| Un dado se lanza dos veces. ¿Cuál es la probabilidad de que la suma de los números sea 7 dado que el primer lanzamiento fue un 3? |
|
Nuestra exploración de la probabilidad condicionada y los sucesos dependientes concluye con una comprensión más profunda de su importancia en la toma de decisiones y la resolución de problemas. Estas herramientas estadísticas brindan una base sólida para analizar y predecir eventos, lo que las hace esenciales en campos como la medicina, las finanzas y la ciencia.
